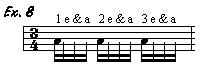The concept of polyrhythms is an often misunderstood topic. This article will
attempt to clarify and explain what polyrhythms are and how they are interpreted
and played. We assume a basic understanding of musical notation and rhythmic
concepts. None of the material is difficult to understand, although if some
of the concepts are new it may take a little while for things to gel. Don't
worry if everything doesn't make sense on the first reading. Try to absorb the
basic concepts and as you become more familiar with polyrhythms things will
start to come together. Polyrhythms are found in just about all types of music.
You may discover that you are already using polyrhythms in your playing. Hopefully
this article will help you further develop your understanding and allow you
to learn and apply new polyrhythms easily.
First we'll begin with a discussion of what a polyrhythm is. A simple definition
of a polyrhythm is two or more rhythms played simultaneously. While this definition
is basically correct, usually when we speak of polyrhythms we are talking about
a more specific relationship between two rhythms. Normally a polyrhythm gives
the impression of one musical pulse being superimposed or played against another.
In other words we have two different rhythms being played against one another
which give the impression of a "cross-rhythm" or "cross-pulse". Perhaps the
easiest way to conceptualize polyrhythms is to think of them as rhythmic ratios.
For example a ratio of 3 notes to 2 notes, or 3:2, would be considered a polyrhythm.
To play such a ratio we must superimpose three notes of equal value over a pulse
of two notes. If the ratio were two notes to three notes (i.e. 2:3) we would
need to superimpose 2 notes of equal value over a pulse of three notes. Generally
two rhythms are only considered a polyrhythm if they have no common divisor
(other than one). In the examples above 2 and 3 have no common divisor. There
is no whole number (other than one) that will divide evenly into both 2 and
3. The rhythmic ratio of 3:4 would also be considered a polyrhythm. Three and
four have no common divisor other than one. On the other hand a rhythmic ratio
of 4 notes to 2 notes (i.e. 4:2) is NOT a polyrhythm. Two and four are both
evenly divisible by two.
Now let's take a look at some specific examples. Here is a ratio of 3:2.
(Ex 1) Three quarter notes (i.e. a quarter note triplet) are being played
over a pulse of 2 quarter notes.

Here is the ratio of 2:3. (Ex. 2) In this example two notes
are being superimposed over a pulse of 3 notes.

Both of the preceding examples are considered polyrhythms. Now let's look
at the ratio of 4:2. (Ex 3) In this example four eighth notes are
being superimposed over two quarter notes.

Ex. 3 is NOT considered a polyrhythm. The eighth notes and quarter
notes line up evenly. What's missing in this example is the characteristic "cross
rhythm" of a true polyrhythm. To say that the eighth and quarter notes line
up evenly is another way of stating that they have a common divisor and therefore
do not qualify as a polyrhythm. Now that we understand what polyrhythms are
let's look at how to play them.
The first step in interpreting any polyrhythm is to find a common denominator
between the two rhythms. We need to have some common note value on which to
interpret both rhythms which make up the polyrhythm. Again let's look at the
example of 3 against 2. (Ex 4)

This ratio means that we are going to play three notes of equal value in the
space of time normally allotted to two notes. The smallest common denominator
of 3 and 2 is 6. Therefore if we subdivide the basic pulse into six equal parts
we will have a common note value on which to interpret both parts of the polyrhythm.
To subdivide the basic pulse into six equal notes we divide the quarter notes
into eighth-note triplets. (Ex 5)

Now we can evenly divide the six notes into two equal parts by playing
every third note. (See Ex. 6 - notes with the stems going down)
We can also divide the six notes into three equal parts by playing every
second note. (Ex 6 - notes with the stems going up)

If we play the two rhythms simultaneously we have the polyrhythm of 3 against
2.
(Note: Only play the notes with the actual note heads. One limb should
play the note heads with the stems going down. Another limb should play
the note heads with the stems going up.)
Let's take another example. Here's the polyrhythm of 4 against 3. (Ex 7)

This ratio means that we are going to play four notes of equal value in the
space of time normally allotted to three notes. The smallest common denominator
of 3 and 4 is 12. Therefore if we subdivide the basic pulse into twelve equal
parts we will have a common note value on which to interpret both parts of the
polyrhythm. To subdivide the basic pulse into twelve equal notes we divide the
quarter notes into sixteenth-notes. (Ex 8)
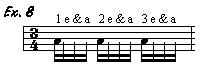
Now we can evenly divide the twelve notes into three equal parts by playing
every fourth note (Ex 9 - stems down) and into four equal parts by playing every
third note (Ex 9 - stems up).

If we play the two rhythms simultaneously we have the polyrhythm of 4 against
3.
If you haven't guessed it by now there is a very simple formula for figuring
out any polyrhythm. The formula can be stated as follows: To play X against
Y divide the Y's into groups of X's and play every Yth one. Let's
take a look at some examples. Here's the 3 against 2 polyrhythm again.
(Ex 10)

In this example we divide the main pulse (the Y's) into groups of three's (groups
of X's). Then we play every 2nd one (every Yth one). Keep in mind that if you
want to play X against Y you should think of Y as your main pulse or point of
reference. In this example the 2's (i.e. the quarter notes) are your main pulse.
By main pulse I mean where you are feeling the beat. Ex 11 and 11-A show
how this may be broken down.


(Remember: Only play the notes with the actual note heads. One
limb should play the note heads with the stems going down. Another limb
should play the note heads with the stems going up. The stems without
note heads are only place holders.)
What we are really doing here is finding the common denominator. By dividing
the quarter note pulse into groups of 3's (triplets) we end up with 6 notes
just as we did when finding the common denominator. Then, one limb can play
every third note and another limb can play every second note to create the polyrhythm.
Let's take a look at a couple more examples. Here's the polyrhythm of 3 against
4. (Ex 12)

We divide the 4's (the quarter notes) into groups of 3's (triplets). Then we
play every 4th one. (See Ex 13 and 13-A)


Here's a slightly more complex polyrhythm of 3 against 5. (Ex 14)

We divide the 5's (the quarter notes) into groups of 3's (triplets). Then we
play every 5th one. (See Ex 15 and 15-A)


Here's the polyrhythm of 5 against 4. (Ex 16)

We divide the 4's (the quarter notes) into groups of 5's (quintuplets). Then
we play every 4th one. (See Ex 17 and Ex 17-A)


Let's end our examples with the polyrhythm of 7 against 5. (Ex 18)

We divide the 5's (the quarter notes) into groups of 7's (septuplets). Then
we play every 5th one. (Ex 19)

So there you have it: To play X against Y, divide the Y's into groups
of X's and play every Yth one. It's as simple as that.
Hopefully this article has shed some light on the concept of polyrhythms. By
using the formula given here you can figure out almost any polyrhythm. Now the
next step is to apply them to various musical settings. As a starting point
listen to some of the masters of polyrhythmic playing. In the jazz area one
of the acknowledged masters is Elvin Jones. Also listen to Jack Dejohnette and
Tony Williams. In the area of rock check out the recordings of Frank Zappa.
Almost all of his drummers have been excellent polyrhythmic players. (Frank
said Vinnie Colaiuta won the prize.) Start with some simple polyrhythms.
Write them out and analyze them. Then begin to incorporate them into your playing.
By incorporating polyrhythms into your own playing you will open up new rhythmic
possibilities and add an increased level of rhythmic sophistication to your
drumming. Good luck and enjoy!
(A future article will look at some practical applications of polyrhythms to
the drumset).
Further Reading:
Fred Albright, Rhythmic Analysis for the Snare Drum
Gary Chaffee, Rhythm and Meter Vol. I
Back
to the main page